Introduction

Quantum Computing proposes with its new approach to do computations a push into new application areas, since it addresses new problem types which so far were out of reach.

Quantum computing is not an entirely new development. Already since the 1980s, explicit formulations of the concept exist. In the 1990s the works of Peter Shor [1] and Lov Grover [2] with their quantum algorithms for the factorization problem and unstructured data base search attracted broad interest.

Since the beginning of the 2000s the quantum algorithm zoo¹ did grow significantly and faster and faster. In the meantime, many important computational problems are addressed by quantum algorithms, which also utilize the ideas of the pioneers of quantum computing.

The 2010s marked a rethinking towards more practical computational problems in particular in the areas of optimization and machine learning, but also concerning the simulation of physical systems. Also in that time, progress in the practical development of quantum computing technology took place, starting with the development of quantum annealers and after 2015 also by the implementation of the increasingly preferred gate model of quantum computing [3]. In the year 2018, John Preskill coined the term „Noisy Intermediate-Scale Quantum“ (NISQ) for the current era of quantum computing [4] with its 50-100 qubit machines without error correction. The limitations of the NISQ era motivated the development of new algorithmic approaches. Increasing efforts have been made e.g. in the areas of supervised machine learning and combinatorial optimization specifically for those machines. Also die development of software frameworks to implement these algorithms accelerated [5].

Modern Quantum Algorithms

The current algorithms are classified as hybrid quantum-classical algorithms or variational circuits [6]. This concept takes care of the limitations of current hardware and is intuitive in this sense: A quantum core of a given problem is implemented as relatively shallow parametrized quantum circuit and a classical computer runs some classical optimization algorithm to optimize the parameters of the quantum circuit. The quantum part and the classical part of this hybrid algorithm run iteratively one after the other and the variation of the parameters in this loop solves the overall problem. The output of the quantum circuit is optimized concerning a given objective function, e.g. by gradient decent or by the application of some other classical optimization method, Figure 1.

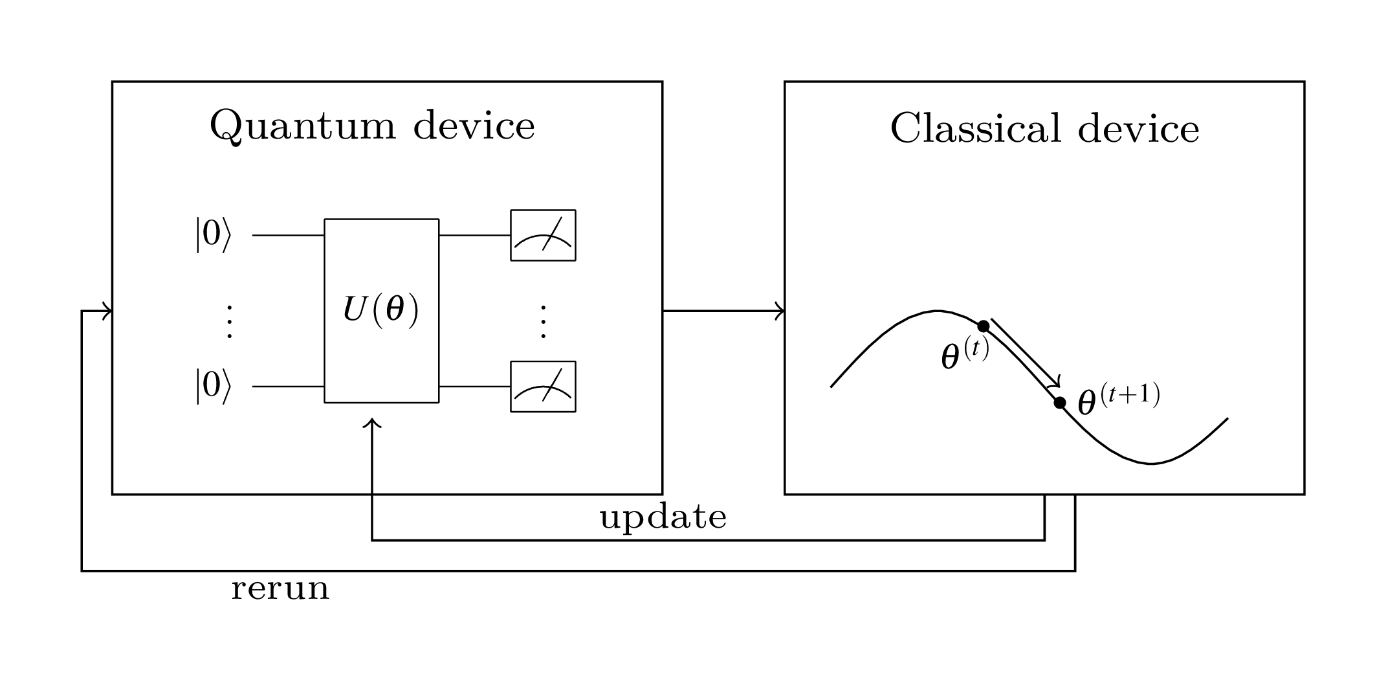
Figure 1: Schematic view of the principle of hybrid quantum-classical algorithms.

The currently most promising quantum algorithms work according to this principle – e.g. VQE (Variational Quantum Eigensolver) [7], different QNN-Variants (Quantum Neural Network) [8] and also QAOA (Quantum Approximate Optimization Algorithm) [9]. Those algorithms feed the three application areas Simulation, Machine Learning and Optimization - three potential application areas of modern quantum algorithms. Explicitely we also mention here solvers for systems of linear equations because of their high practical relevance. The applications are various. One example is the efficient implementation of finite element methods [10] and the HHL algorithm promises significant potentials to embody this approach. And also here, hybrid algorithms can help [11].

Quantum Software Frameworks

Besides the progress with quantum algorithms, in particular developments in the subject of quantum programming languages are good news, e.g. Q#, Silq or simply the pragmatic integration of quantum computing artefacts in Python. Quantum programming also relies significantly on the application of powerful simulators to test and evaluate new algorithms².

This drives together with the rapidly improving hardware the development of more and more quantum software frameworks (e.g. Forest SDK³, Cirq⁴, Qiskit⁵), as well as the provision of cross-platform cloud services, which offer quantum computing based on simulators or based on real hardware as a service (e.g. Azure Quantum⁶, amazon Bracket⁷).

Additionally to the frameworks that have been already mentioned, there is also a series of developments of frameworks for specific topics, e.g. for Quantum Artificial Intelligence or Quantum Machine Learning (e.g. PennyLane⁸, TensorFlow Quantum⁹). Particular frameworks address also increasingly specific application areas, e.g. Qiskit with modules for natural sciences, finances, optimization and Machine Learning. In future, hybrid strategies will also merge quantum computing approaches and classical HPC and new approaches for the programming of quantum machines will improve the usability when implementing algorithms, going beyond quantum circuits towards higher concepts.

Literature

[1] Shor, P. W. "Polynomial-time algorithm for prime factorization and discrete logarithms on a quantum computer: proc."35th Annual Symp. on the Foundations of Computer Science. Vol. 124. 1994.

[2] Grover, Lov K. "A fast quantum mechanical algorithm for database search."Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. 1996.

[3] Debnath, Shantanu, et al. "Demonstration of a small programmable quantum computer with atomic qubits."Nature 536.7614 (2016): 63-66.

[4] Preskill, John. "Quantum Computing in the NISQ era and beyond." Quantum 2 (2018): 79.

[5] Schuld, Maria, and Francesco Petruccione. "Learning with Quantum Models."Supervised Learning with Quantum Computers. Springer, Cham, 2018. 247-272.

[6] McClean, Jarrod R., et al. "The theory of variational hybrid quantum-classical algorithms." New Journal of Physics 18.2 (2016): 023023.

[7] Parrish, Robert M., et al. "Quantum computation of electronic transitions using a variational quantum eigensolver." Physical review letters 122.23 (2019): 230401.

[8] Farhi, Edward, and Hartmut Neven. "Classification with quantum neural networks on near term processors." arXiv preprint arXiv:1802.06002 (2018).

[9] Farhi, Edward, Jeffrey Goldstone, and Sam Gutmann. "A quantum approximate optimization algorithm."arXiv preprint arXiv:1411.4028 (2014).

[10] Montanaro, Ashley, and Sam Pallister. "Quantum algorithms and the finite element method."Physical Review A 93.3 (2016): 032324.